Detecting Extreme Events in Lévy processes

In our paper we develop a length scale $L_{\text{b}}$ that we call the "bifurcation length". Below is a plot of this $L_{\text{b}}$ in the natural units $\sigma T^{1/\alpha}$ of a Levy process, where $\sigma$ is the width parameter, $\alpha$ is the stability index, and $T$ is the evolution time.

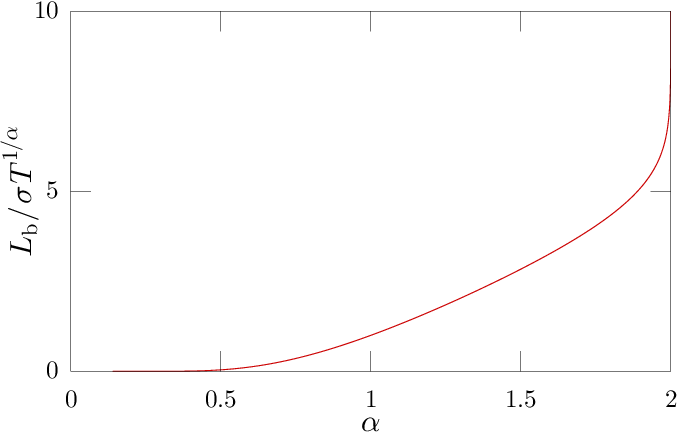
Notice that $L_{\text{b}}$ diverges as $\alpha\rightarrow 2$, demonstrating that this is indeed a scale that is distinct from the natural length scale.

To see the effectiveness of this scale for detecting extreme events, below I show a plot of a Levy process sample path ($\Delta t=T/500$ with $\alpha=1.9$) with certain "extreme" steps highlighted. You can highlight steps based on the bifurcation-length criteria ($\Delta x > L_{\text{b}}(\Delta t/T)^{1/\alpha}$) or a more naive criteria ($\Delta x > \sigma(\Delta t/T)^{1/\alpha}$) by hovering your mouse over the corresponding indicator.

• No Highlights
• $\Delta x > L_{\text{b}}(\Delta t/T)^{1/\alpha}$
• $\Delta x > \sigma(\Delta t/T)^{1/\alpha}$

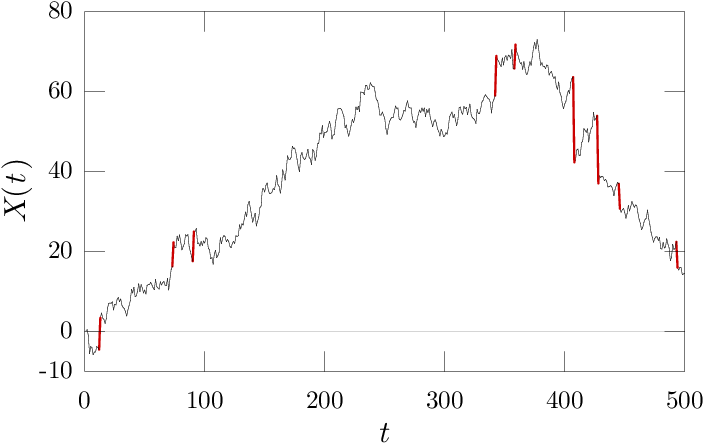
Qualitatively, we see that steps that appear "extreme" are well indicated by the bifurcation-length based criteria, while the naive criteria selects many steps that do not appear to be extreme by eye.

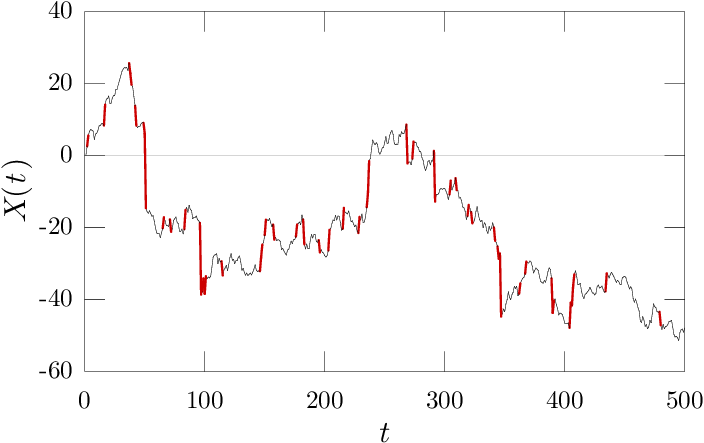
This also work for other values of $\alpha$, ($\alpha=1.5$ shown below), though as $\alpha$ approaches $1$ both the bifurcation-length based criteria and the naive criteria indicate the same steps as "extreme".

• No Highlights
• $\Delta x > L_{\text{b}}(\Delta t/T)^{1/\alpha}$
• $\Delta x > \sigma(\Delta t/T)^{1/\alpha}$

For the derivation and justification of this scale, see our paper here.